अभाज्य संख्याको यो महत्व !
अभाज्य संख्या शुरू त १ बाटै हुन्छ, तर यो कतिसम्म ठूलो हुन सक्छ भन्ने अझै टुंगो लागेको छैन। भर्खरै वैज्ञानिकहरूले पत्ता लगाएको, अहिलेसम्मको सबैभन्दा ठूलो अभाज्य संख्या करीब साढे दुई करोड वटा अंकको छ। तर केमा काम लाग्छ यस्तो अजिंगरे संख्या ? के हो, अभाज्य संख्याको उपयोगिता र महत्व ?
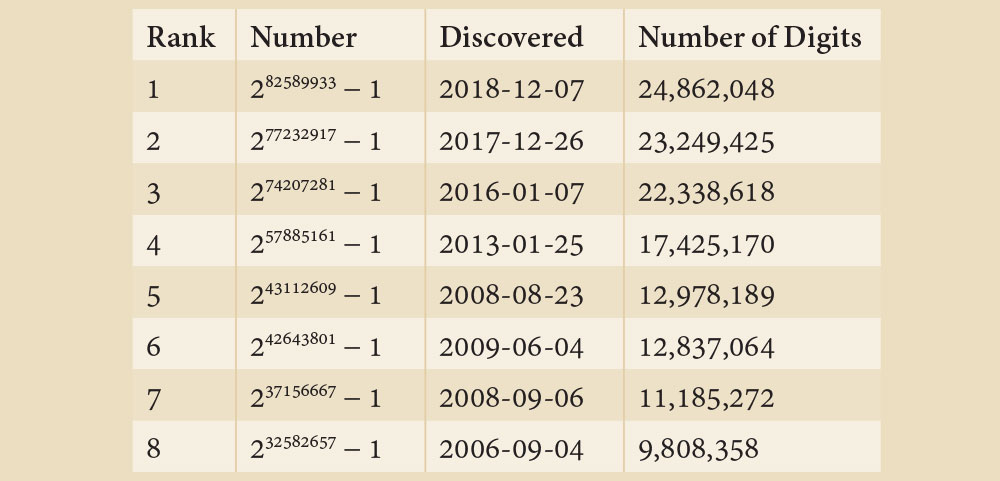
केही महीना अघि खबर आयो— वैज्ञानिकहरूले अहिलेसम्मको सबैभन्दा ठूलो अभाज्य संख्या पत्ता लगाएका छन् । त्यो संख्या हो— २८,२५,८९,९३३–१ । यो संख्यालाई यहाँ सामान्य ढंगबाट लेखेर देखाउन सकिंदैन किनभने त्यसमा २ करोड ४८ लाख ६२ हजार ४८ वटा अंक छन् । त्यति वटा अंक एक पानामा २५०० अंकका दरले लेख्तै जाने हो भने झन्डै दश हजार पाना भरिन्छन् । अघिल्लो वर्षसम्म सबैभन्दा ठूलो अभाज्य संख्या २७,७२,३२,९१७–१ थियो । तर, वैज्ञानिकहरू किन ठूलोभन्दा ठूलो अभाज्य संख्या पत्ता लगाउन मरिमेटेर लागिपर्छन् ?
पहिले अभाज्य (Prime Number) संख्या के हो भन्ने नै बुझैं । अभाज्य (कसैले अविभाज्य पनि भनेको पाइन्छ) संख्या त्यो प्राकृत संख्या हो, जो केवल १ र स्वयं त्यही संख्याद्वारा मात्र पूर्णतः विभाजित हुन सक्छ, यी बाहेक अरू संख्याद्वारा भाग जान सक्तैन । जस्तै– २,३,५,७,११,१७... आदि हामीले जान्दै आएका साना अभाज्य संख्या हुन् । अभाज्य संख्या अनन्त छन् । यिनका केही विशेषता छन् । त्यसै कारण यिनको विशेष उपयोगिता छ ।
स्वास्थ्य, चिकित्सा अथवा प्रविधिका क्षेत्रमा नयाँ आविष्कारको समाचार सुन्दा हाम्रो मनमा यस्तो खोजको के आवश्यकता भन्ने प्रश्न उठ्तैन । तर, जब वैज्ञानिकहरूले पहिलेभन्दा ठूलो अभाज्य संख्या पत्ता लगाए भन्ने खबर सुन्छौं, मनमा प्रश्न उठ्छः यति ठूलो संख्या किन पत्ता लगाउनु परेको होला ? यति ठूलो, त्यसमाथि अभाज्य, संख्या त हामी आफ्नो जीवनमा कहिल्यै प्रयोग पनि गर्दैनौं !
वास्तविकता यसको विपरीत छ । प्रत्यक्ष रूपमा नभए पनि आजभोलि यी संख्याहरूको अप्रत्यक्ष रूपमा हामी भरपूर उपयोग गर्छौं । आज हामी टेलिफोन, इन्टरनेट, क्रेडिट कार्ड, एटीएम, स्मार्ट फोन, गेम्स, ह्वाट्सएप जस्ता म्यासेन्जर एप्स आदिको प्रयोग गर्छौं र यिनको उपयोग दिनानुदिन बढ्दै गएको छ । यस्ता प्रविधिको निश्चितताका साथ, सुरक्षित तरीकाले उपयोग गर्न पाउनुको श्रेय, ठूलो मात्रामा, अभाज्य संख्याहरूलाई नै जान्छ । यस्ता उपकरण र प्रविधिको उपयोग हामी जति बढी गर्छौं, उति नै बढी हाम्रा महत्वपूर्ण डेटा डिजिटल रूपमा स्टोर र ट्रान्सफर हुँदै जान्छन् । यस्ता सूचना अथवा डेटा संवेदनशील एवं महत्वपूर्ण हुन्छन्, त्यसैले तिनलाई सुरक्षित राख्नु पनि जरूरी हुन्छ । डेटालाई सुरक्षित राख्न विभिन्न कूटलेखन–सूत्रविधिहरू (Algorithm) को सहारा लिइन्छ । कूटलेखन (एल्गोरिदम) भनेको कुनै सूचना वा सन्देशलाई गोप्य–सन्देश (सिक्रेट म्यासेज) मा बदल्ने तरीका हो, जसले गर्दा त्यो सन्देश वाञ्छित व्यक्तिले मात्र पढ्न/बुझन सक्छ । यस्ता कूटलेखन–सूत्रविधिको निर्माणमा अभाज्य संख्याहरूको अहम् भूमिका हुन्छ ।
सुरक्षित तरीकाले सन्देश पठाउन प्रायः आरएसए एल्गोरिदम को उपयोग गरिन्छ । यसमा दुई वटा कुन्जी (Key) को प्रयोग हुन्छ— सार्वजनिक (पब्लिक) कुन्जी र निजी (प्राइभेट) कुन्जी । नाम अनुरूप नै सार्वजनिक कुन्जी सबैलाई थाहा हुन्छ र निजी कुन्जी गुप्त राखिन्छ । दुवै कुन्जी सन्देश प्राप्त गर्नेले निर्माण गरेको हुन्छ । उसले सार्वजनिक कुन्जी त सबैलाई थाहा दिन्छ, तर निजी कुन्जी आफूसँगै गोप्य राख्छ । सन्देश पठाउनुपर्दा उसको सार्वजनिक कुन्जीको माध्यमबाट सन्देशलाई कूटबद्ध गरिन्छ । त्यसरी पठाइएको सन्देश प्रापकले आफ्नो निजी कुन्जीको माध्यमबाट पढ्छ ।
कुन्जी निर्माण र सन्देश
सार्वजनिक कुन्जीमा दुई वटा संख्या हुन्छन् । यीमध्ये पहिलो संख्या कुनै दुई अभाज्य संख्याहरूको गुणनफल हुन्छ । दोस्रो संख्या तिनै दुई अभाज्य संख्याहरूका आधारमा निर्धारित हुन्छ । यहाँ हामी सार्वजनिक कुन्जीका उक्त संख्यालाई क्रमशः N र e भनेर अनि निजी कुन्जीलाई म भनेर सम्बोधन गर्नेछौं । आउनुहोस्, एउटा उदाहरण मार्फत यी कुन्जीको निर्माण प्रक्रिया र कुन्जी मार्फत सन्देश पठाउने–पढ्ने प्रक्रिया बुझने प्रयास गरौंः
N को चयनः
क. सर्वप्रथम कुनै दुई अभाज्य संख्या लिने । मानौं, हामीले ११ र १७ लियौं ।
ख. दुवै अभाज्य संख्यालाई आपसमा गुणा गर्ने । त्यसबाट प्राप्त गुणनफल N हुन्छ । (११x१७=१८७) यसप्रकार यहाँ N १८७ भयो ।
e को चयनः
क. सर्वप्रथम शुरूमा छानिएका दुवै अभाज्य संख्याबाट एक–एक घटाउने । (११–१=१०, १७–१×=१६)
ख. यसरी हुन आउने दुवै संख्यालाई आपसमा गुणा गर्ने । (१०x१६=१६०)
(प्राप्त गुणनफललाई हामी Q भन्छौं । यहाँ Q= १६०) छ ।)
ग. e का लागि एउटा यस्तो संख्या चुनिन्छ, जो Q भन्दा सानो हुन्छ र त्यसले त्त लाई पूरापूर भाग लाग्दैन ।
यहाँ Q १६० छ । त्यसैले e का लागि १६० भन्दा सानो कुनै पनि संख्या चुन्न सकिन्छ, जसबाट Q अर्थात् १६० पूर्ण विभाजित नहोस् । मानौं, हामी e का लागि ७ लाई चुन्छौं ।
यसप्रकार सार्वजनिक कुन्जी भयो— N=१८७, भ=७ ।
d को चयनः
क. सर्वप्रथम त्त मा १ जोड्ने । (१६०+१=१६१)
ख. यसरी प्राप्त हुने संख्यालाई Q ले भाग दिने । प्राप्त भागफल नै म हो ।
यहाँ १६१ लाई e अर्थात् ७ ले भाग दिंदा भागफल २३ हुन्छ । त्यसैले निजी कुन्जी भयो—d=२३ ।
कूटलेखन
सन्देश पठाउने क्रममा, सर्वप्रथम, पठाउन लागिएको सन्देशलाई कुनै एल्गोरिदमको सहायताले संख्यामा बदलिइन्छ । त्यसपछि सार्वजनिक कुन्जीको सहायताले सन्देशलाई कूट–सन्देशमा रूपान्तरित गरिन्छ । यसरी पठाइएको सन्देश प्रापकले निजी कुन्जीको सहायताले खोल्छ र पढ्छ ।
मानिलिऊँ, पठाउन लागिएको सन्देश ३ हो (कुनै एल्गोरिदमको मदतले संख्यामा बदलिएको) । यहाँ सार्वजनिक कुन्जी १८७ (N) र ७ (e) छ ।
क. सन्देशलाई कूट बनाउन सन्देशको संख्यालाई त्यही संख्याले भ को संख्या बराबर पटक गुणा गरिन्छ । तदनुसार यहाँ ३ लाई ३ ले ७ पटक गुणा गर्नुपर्छ (३x३x३x३x३x३x३) । यसरी गुणा गर्दा गुणनफल २१८७ निस्कन्छ ।
ख. प्राप्त संख्यालाई N ले भाग गरिन्छ । यसरी भाग गर्दा जे शेषफल बाँकी रहन्छ, त्यसैलाई सन्देशका रूपमा पठाइन्छ । यहाँ २१८७ लाई १८७ ले भाग गर्दा १३० शेषफल बाँकी हुन्छ । त्यसैले, पठाइने कूट सन्देश हो— १३० ।
ग. पठाइएको कूट सन्देश निजी कुन्जी (d) को मदतले खोलेर पढिन्छ । हाम्रो निजी कुन्जी हो— २३ । कूट सन्देश खोल्न सर्वप्रथम त्यसको संख्यालाई त्यही संख्याले म को संख्या बराबर पटक गुणा गरिन्छ । तदनुसार यहाँ १३० लाई १३० ले २३ पटक गुणा गर्नुपर्छ ।
घ. यसबाट प्राप्त हुने संख्यालाई N ले भाग गरिन्छ । यसरी भाग गर्दा जे शेषफल बाँकी रहन्छ, त्यही सन्देश हुन्छ । यहाँ कूट सन्देशको संख्यालाई त्यही संख्याले d को संख्या बराबर अर्थात् (१३० लाई १३० ले २३ पटक गुणा गर्दा आउने अंक हो— ४१७५३९०५ x १०४१ । यस संख्यालाई N अर्थात् १८७ ले भाग गर्दा शेषफल ३ बाँकी रहन्छ । पठाइएको सन्देश यही हो ।
ठूला अभाज्य संख्या
यहाँ हामीले उदाहरणका लागि साना अभाज्य संख्या (११ र १७) को चयन गर्यौं । वास्तविक कूट सन्देशका लागि चयन गरिने यस्ता संख्या निकै ठूला हुने गर्छन् ।
प्रश्न उठ्छ, ठूला अभाज्य संख्या नै किन ? वस्तुतः एक भन्दा बढी कुनै पनि संख्याका गुणनखण्ड अभाज्य संख्याहरूका रूपमा प्राप्त गर्न सकिन्छन् । उदाहरणका लागि ७० लाई २x७ का रूपमा लेख्न सकिन्छ । यिनलाई अभाज्य गुणनखण्ड भनिन्छ । गणितज्ञहरूका अनुसार, कुनै पनि दुई ठूला अभाज्य संख्याहरूको गुणनफल पत्ता लगाउन त सजिलो छ, तर तिनको अभाज्य गुणनखण्ड पत्ता लगाउन ज्यादै कठिन छ । मान्छेको त के कुरा, सुपर कम्प्युटरलाई समेत यस्ता अंक पत्ता लगाउन कठिन भइरहेको छ । ज्यादै ठूला संख्याहरूको अभाज्य गुणनखण्ड पत्ता लगाउनै सकिंदैन भन्ने चाहिं होइन । तर यसका लागि धेरै लामो समय लाग्छ, शायद कैयौं वर्ष । त्यसैले, अभाज्य संख्या जति ठूला हुन्छन्, डेटा उति सुरक्षित हुन्छन् । वैज्ञानिकहरू ठूलोभन्दा ठूलो अभाज्य संख्या पत्ता लगाउन मरिमेटेर लागिपर्नुको कारण यही हो ।
कूटलेखनको उपयोग इन्टरनेटका माध्यमबाट हुने पैसाको लेनदेनको सुरक्षामा; निश्चित समयमा सन्देश पुर्याउन; सूचना पठाइने व्यक्तिको प्रमाणीकरण अथवा सत्यापन (डिजिटल सिग्नेचर) मा; क्रेडिट कार्ड, एटीएम, ईमेल, स्टोरेज, डिभाइसको सुरक्षा आदिमा हुन्छ । यी सबै ठाउँमा अभाज्य संख्याको उपयोग हुन्छ ।
यसबाहेक, र्यान्डम नम्बर निकाल्ने एल्गोरिदम मा अभाज्य संख्याको उपयोग हुन्छ । अर्थात्, जहाँ संख्याहरूको अव्यवस्था आवश्यक हुन्छ, त्यहाँ यसले काम गर्छ । जस्तै, सुरक्षित लेनदेन (वन टाइम पासवर्ड) का लागि ओटीपी नम्बर निकाल्न, अनलाइन क्यासिनोमा तासका पत्ती निकाल्न अथवा पासामा आउने संख्या तय गर्न आदि । इन्टरनेटमा बनेको कुनै पनि अकाउन्टमा लगइन गर्दा पासवर्ड मिलान गरिन्छ । यो काम न्यूनतम समयमा पूरा गर्नुपर्ने हुन्छ त्यसैले ह्याश–टेबल ९ज्बकज तबदभि० को मदत लिइन्छ । ह्याशटेबलले पनि अभाज्य संख्याकै आधारमा काम गरिरहेको हुन्छ । यसले वेबसाइटमा कुनै पनि कुरा छिट्टै खोजेर निकाल्नुका अतिरिक्त सर्फिङ र सर्चिङ (जस्तै शपिङ) मा पनि सहयोगीको भूमिका खेल्छ । क्यान्डीक्रस जस्ता अनेकौं खेल रचना गर्न पनि अभाज्य संख्याहरूकै उपयोग गरिएको हुन्छ । अचम्मको कुरा त के भने कतिपय कीटले समेत अभाज्य संख्याकै पद्धति प्रयोग गरेर आफू र आफ्नो प्रजातिलाई शिकारीबाट सुरक्षित राख्ने गरेको पाइन्छ ।
सार कुरो के भने, आधुनिक सूचना–प्रविधिको उपयोग गर्दा हामी अभाज्य संख्याहरूको थाहै नपाई उपयोग गरिरहेका हुन्छौं । आधुनिक दुनियाँलाई बढी सहज, भरपर्दो र सुरक्षित बनाउन यिनले अतुलनीय भूमिका खेलेका छन् । अनि किन अभाज्य संख्याको पछि नलागुन् त वैज्ञानिकहरू ?
साभारः स्रोत फिचर्स, अक्टोबर २०१९
भाषान्तरः शरच्चन्द्र वस्ती
शिक्षक मासिक, २०७६ माघ अंकमा प्रकाशित ।




